1. 문제해결 시나리오

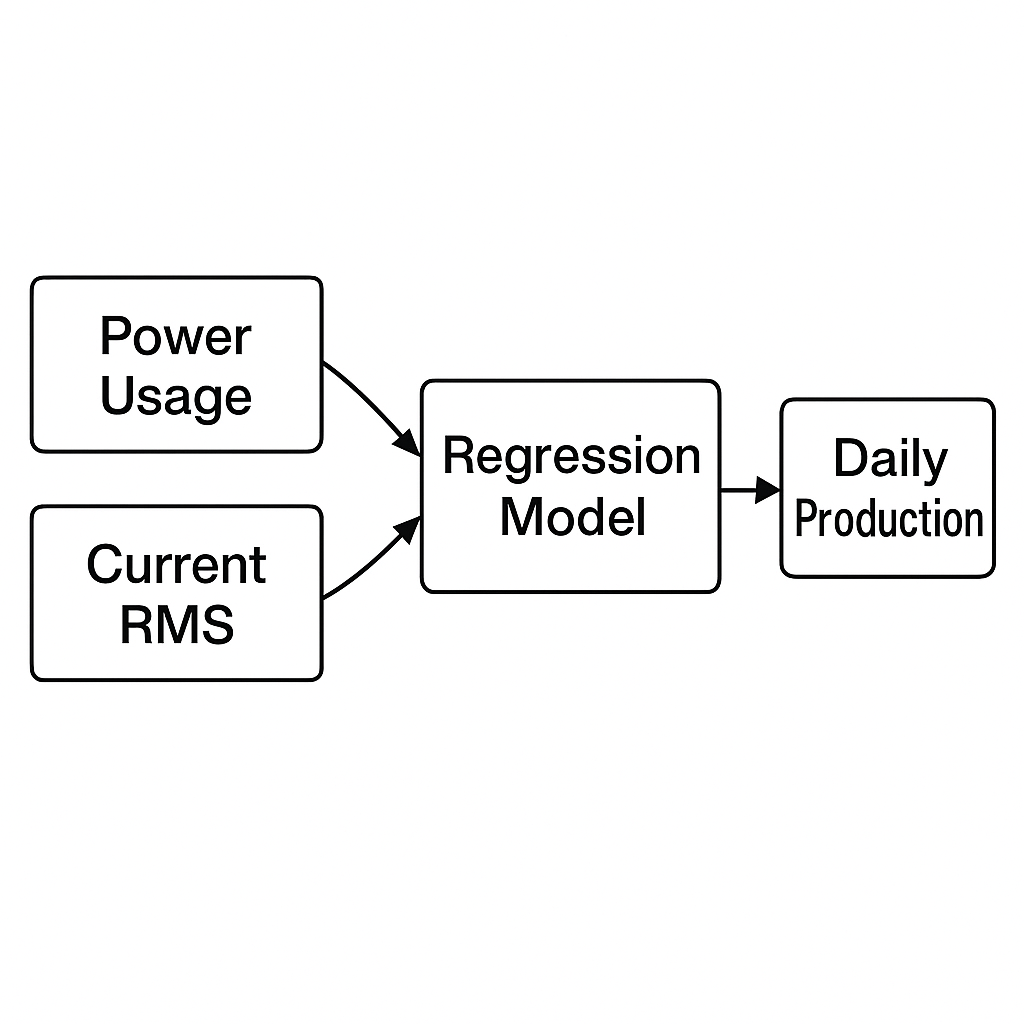
어느 식품 제조 회사에서는 하루 동안의 생산 전력 사용량과 전류 RMS 데이터를 수집하고, 동시에 하루 생산 수량을 자동으로 합산해 약 120일치 데이터를 DB에 저장해두고 있다.
이 데이터를 기반으로, 하루 동안 생산에 소비한 전력 패턴을 분석하여 그날의 생산량을 예측하는 회귀 알고리즘을 구축할 수 있다.
즉, 전력 사용량과 전류 RMS(평균·최대값 등)를 입력으로 사용하고, 하루 생산량을 출력으로 하는 모델을 만들면, 전력 대비 생산 효율을 정량적으로 평가하고 향후 생산량을 사전에 예측할 수 있는 환경이 구성된다.
2. 시나리오 임의 데이터 셋 준비
※ 문제해결 시나리오를 기반으로 임의의 데이터 셋을 준비한다.
day power_kwh current_rms_avg current_rms_max production_qty
1 412 5.8 11.2 980
2 398 5.5 10.7 950
3 421 5.9 11.5 1005
4 445 6.1 11.9 1040
5 462 6.3 12.2 1080
6 455 6.2 12.1 1065
7 438 6 11.8 1020
8 470 6.4 12.4 1100
9 489 6.6 12.8 1145
10 501 6.8 13 1180
11 510 6.9 13.3 1195
12 528 7.1 13.5 1235
13 540 7.3 13.7 1260
14 533 7.2 13.6 1248
15 520 7 13.4 1220
16 505 6.8 13 1188
17 480 6.4 12.5 1130
18 468 6.3 12.3 1105
19 452 6.1 11.9 1078
20 439 6 11.7 1045
21 430 5.9 11.5 1030
22 458 6.2 12.1 1095
23 472 6.4 12.4 1120
24 485 6.5 12.6 1150
25 499 6.7 12.9 1180
26 515 6.9 13.2 1205
27 528 7.1 13.4 1240
28 544 7.3 13.8 1265
29 558 7.4 14 1290
30 573 7.6 14.3 1330
31 589 7.8 14.6 1360
32 598 7.9 14.7 1380
33 610 8.1 15 1405
34 622 8.2 15.3 1430
35 630 8.3 15.4 1448
36 618 8.1 15.1 1410
37 605 7.9 14.8 1380
38 590 7.8 14.6 1360
39 578 7.6 14.3 1330
40 560 7.5 14.1 1305
41 545 7.3 13.9 1270
42 532 7.2 13.7 1245
43 521 7 13.4 1220
44 505 6.8 13 1185
45 492 6.6 12.8 1160
46 480 6.5 12.6 1130
47 468 6.4 12.3 1100
48 450 6.2 12.1 1070
49 441 6.1 11.9 1045
50 430 5.9 11.6 1020
51 420 5.8 11.4 995
52 435 6 11.8 1030
53 448 6.2 12 1050
54 465 6.3 12.3 1090
55 475 6.5 12.6 1120
56 490 6.6 12.8 1150
57 503 6.8 13 1180
58 515 6.9 13.2 1210
59 528 7 13.4 1235
60 545 7.2 13.7 1265
61 558 7.4 14 1295
62 570 7.5 14.2 1320
63 585 7.7 14.4 1350
64 598 7.9 14.7 1380
65 610 8 14.9 1400
66 622 8.2 15.1 1430
67 635 8.4 15.3 1455
68 648 8.5 15.5 1480
69 659 8.7 15.7 1505
70 670 8.8 16 1530
71 682 9 16.2 1560
72 695 9.2 16.5 1595
73 708 9.3 16.7 1620
74 720 9.5 17 1650
75 735 9.7 17.2 1680
76 748 9.8 17.4 1705
77 760 10 17.6 1730
78 772 10.1 17.8 1755
79 785 10.3 18 1780
80 798 10.5 18.3 1810
81 810 10.6 18.5 1835
82 823 10.8 18.7 1860
83 838 11 19 1890
84 850 11.1 19.2 1915
85 860 11.2 19.3 1930
86 872 11.3 19.5 1950
87 885 11.5 19.7 1980
88 899 11.7 20 2010
89 910 11.8 20.2 2030
90 925 12 20.5 2060
91 935 12.1 20.7 2080
92 950 12.3 21 2105
93 965 12.5 21.2 2140
94 980 12.7 21.5 2175
95 995 12.8 21.8 2200
96 1010 13 22 2235
97 1025 13.1 22.2 2260
98 1035 13.3 22.5 2285
99 1050 13.5 22.7 2310
100 1065 13.6 22.9 2340
101 1080 13.8 23.2 2375
102 1095 14 23.5 2400
103 1110 14.1 23.7 2430
104 1120 14.3 23.9 2450
105 1135 14.4 24.1 2475
106 1150 14.6 24.3 2500
107 1165 14.8 24.6 2530
108 1180 14.9 24.8 2555
109 1195 15 25 2580
110 1210 15.2 25.3 2610
111 1225 15.4 25.6 2640
112 1240 15.5 25.8 2665
113 1255 15.6 26 2688
114 1270 15.8 26.2 2710
115 1285 16 26.5 2745
116 1300 16.1 26.7 2770
117 1315 16.3 27 2800
118 1330 16.5 27.2 2830
119 1345 16.6 27.4 2850
120 1360 16.8 27.6 28803. Python 코드

# 우선 Matplotlib으로 시각화 해본다.
import pandas as pd
import matplotlib.pyplot as plt
# CSV 불러오기
df = pd.read_csv("production_energy_dataset.csv")
plt.figure(figsize=(14, 10))
# 1) 하루 전력 사용량
plt.subplot(3, 1, 1)
plt.plot(df["day"], df["power_kwh"], linewidth=2)
plt.title("Daily Power Usage (kWh)")
plt.xlabel("Day")
plt.ylabel("kWh")
plt.grid(True)
# 2) 전류 RMS 평균 / 최대값
plt.subplot(3, 1, 2)
plt.plot(df["day"], df["current_rms_avg"], label="RMS Avg", linewidth=2)
plt.plot(df["day"], df["current_rms_max"], label="RMS Max", linewidth=2)
plt.title("Current RMS (Avg & Max)")
plt.xlabel("Day")
plt.ylabel("RMS")
plt.legend()
plt.grid(True)
# 3) 생산량
plt.subplot(3, 1, 3)
plt.plot(df["day"], df["production_qty"], color="black", linewidth=2)
plt.title("Daily Production Quantity")
plt.xlabel("Day")
plt.ylabel("Production Qty")
plt.grid(True)
plt.tight_layout()
plt.show()시각화 ( Matplotlib ) 주요 메서드 복습
plt.plot() : 선 그래프 생성
plt.scatter() : 산점도(scatter plot) 생성
plt.bar() : Bar 차트 생성
plt.figure(figsize=(w,h)) : 그래프 캔버스 크기 설정
plt.title() : 그래프 제목 표시
plt.xlabel() : x축 텍스트 라벨
plt.ylabel() : y축 텍스트 라벨
plt.grid(True) : 그래프에 격자 표시
plt.legend() : 그래프에 범례 표시
plt.show() : 생성된 그래프 화면에 출력
선형 회귀란?
선형 회귀는 입력 특성(Feature) 과 타깃(Target) 사이의 관계를 직선(1차 함수) 으로 모델링하는 가장 기본적인 머신러닝 알고리즘이다.
직선의 형태는 다음과 같다.
y = ax+b
- x: 입력 특성
- y: 예측값
- a: 기울기(가중치, weight)
- b: 절편(bias)
즉, “x가 커지면 y가 어떻게 변하는지”를 직선의 기울기(a)로 표현하는 방식이다.
특성이 하나라면 단순 선형 회귀, 특성이 여러 개라면 다중 선형 회귀
지금은 전력 사용량, RMS 평균, RMS 최대를 특성으로 사용할 예정이기 때문에
y=w1x1+w2x2+w3x3+b
형태는 여전히 선형(1차 함수)
단지 특성이 여러 개라서 직선이 고차원 공간에 존재하는 것이다.
즉, 차원이 높아질 뿐 원리는 같다.
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, r2_score
# CSV 읽기
df = pd.read_csv("production_energy_dataset.csv")
# 입력(X), 출력(y) 정의
X = df[["power_kwh", "current_rms_avg", "current_rms_max"]]
y = df["production_qty"]
# train/test 분리
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# 선형 회귀 모델 생성
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 평가
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("MAE:", mae)
print("R² Score:", r2)
# 회귀 계수
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)
1. MAE (Mean Absolute Error) = 6.51
MAE가 6.5개라는 의미는, 하루 생산량 예측 시 평균적으로 약 6~7개 정도만 오차가 발생한다는 뜻. 전체 생산량이 1,000 ~ 3,000개 수준인 점을 고려하면 오차율은 0.3~0.6% 수준의 매우 낮은 오차. 실제 공정 예측 모델로 사용해도 될 만큼 정확도가 매우 높음을 의미한다.
2. R² Score = 0.9997
1에 가까울수록 "모델이 데이터를 거의 완벽하게 설명"한다는 뜻. R² = 0.9997 → 99.97%의 설명력, 이는 엄청나게 높은 수치. 에너지 패턴(전력 사용량 + RMS값)이 생산량과 거의 완벽한 선형 관계를 가진다는 것을 의미함.
즉, 전력/전류의 조합이 생산량을 정량적으로 매우 잘 설명한다는 강력한 증거
이 공장에서는 생산량과 에너지 소비의 관계가 상당히 선형적임을 확인할 수 있음
3. Coefficients (회귀 계수) 분석
- 전력(kWh)의 계수가 거의 0에 수렴(-0.008)
→ 전력 사용량은 실제로는 "생산량과 직접적 선형 관계가 약하다"고 해석 가능
→ 대신 RMS(전류 패턴)가 생산량과 매우 강한 관계를 가짐- RMS 평균(Avg)이 가장 영향력이 크다 (+87.6)
→ 설비가 일하는 실제 부하 패턴을 가장 잘 반영하는 특성- RMS 최대(Max)도 강한 양의 기여 (+56.9)
→ 장비 피크 부하가 생산량 증가에 어느 정도 비례하는 구조
하지만 현실 데이터는 항상 직선일까?
절대 그렇지 않다.
특히
- 전력 소비량과 생산량
- 온도와 품질 변화
- 시간에 따른 센서 값 변화
- 공정 장비의 부하와 생산 속도
이런 실제 산업 데이터는 대부분 비선형(Non-linear) 이다.
예를 들어:
- 전력 사용량이 증가한다고 생산량이 항상 비례해 증가하지 않는다.
- 어느 지점부터는 효율이 떨어져 곡선 형태가 나타남.
- 센서 값들은 주기적인 패턴(곡선)을 많이 포함한다.
그리고 선형 회귀의 가장 큰 단점은 예측 값이 음수로 나올 수가 있다. (당연하게도 직선그래프이기 때문이다.)
생산량의 예측의 경우 음수가 도출되면 안된다.
매출 예측의 경우에도 음수가 도출되면 안된다.
인구수 예측의 경우에도 음수가 도출되면 안된다.
이런 데이터는 선형 회귀를 그대로 쓰면 값이 현실을 벗어날 수 있다.
그래서 등장하는 방법: 다항 회귀(Polynomial Regression)
다항 회귀는 선형 회귀의 확장판이다.
직선(1차식)으로는 설명이 부족하므로, 모델에 곡선 형태(2차, 3차…) 를 추가하는 방식이다.2차식(Quadratic)
y=a2x2+a1x+by = a_2x^2 + a_1x + b
3차식(Cubic)
y=a3x3+a2x2+a1x+by = a_3x^3 + a_2x^2 + a_1x + b
선형 회귀는 "직선"으로만 예측한다.
하지만 제조 데이터는 다음처럼 곡선적 패턴이 많다:
- 전력량이 증가하다 일정 시점에서 포화됨
- RMS 전류가 일정 수준을 넘으면 효율 저하
- 장비의 부하가 낮을 때·높을 때의 패턴이 달라짐
이런 경우 곡선을 학습할 수 있는 다항 회귀가 훨씬 현실적이다.
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score
# 데이터 불러오기
df = pd.read_csv("production_energy_dataset.csv")
# 입력/출력 분리
X = df[["power_kwh", "current_rms_avg", "current_rms_max"]]
y = df["production_qty"]
# train / test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 다항 차수
poly = PolynomialFeatures(degree=2)
# 변환
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)
# 모델 생성
model = LinearRegression()
model.fit(X_train_poly, y_train)
# 예측
y_pred = model.predict(X_test_poly)
# 성능 평가
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("Polynomial Regression Results")
print("MAE:", mae)
print("R² Score:", r2)
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)
1. MAE = 4.40
선형 회귀의 MAE = 6.51보다 오차가 더 낮아짐 하루 생산량이 1000~2800 범위이므로,
오차 4개 이하면 매우 우수한 모델
2. R² = 0.99987
선형 회귀 R² = 0.99973보다 더 높음
전체 변동성의 99.987%를 설명함
공장 생산량 예측 모델이 거의 완벽에 가까운 수준

지금은 다항 회귀 모델이 더 좋은 결과를 만들었지만, 선형 회귀가 더 유리한 경우도 있다.
입력과 출력이 정말 선형적인 관계를 가질 경우에는 선형 회귀가 더 유리하다.
예를 들어 전력 사용량이 1증가하면 생산량이 0.9 증가하는 형태가 명확하다면
선형 회귀가 더 빠르고 정확할 것이다.
'임베디드 AI > TinyML' 카테고리의 다른 글
| K-최근접 이웃 (K-NN) 회귀 알고리즘 (0) | 2025.11.18 |
|---|---|
| TinyML (온 디바이스 AI) (0) | 2025.11.14 |
| K-최근접 알고리즘02 (훈련세트/테스트세트) (0) | 2023.01.24 |
| 머신러닝 알고리즘 분류 (지도학습/비지도학습/강화학습) (0) | 2023.01.24 |
| 머신러닝 K-최근접 이웃 알고리즘(K-Nearest Neighbors) (0) | 2023.01.24 |



