자료구조 (Data Structure)

1. 자료구조 (Data Structure) 개념

https://www.makarablue.com/2023/01/what-is-data-structure.html

자료구조(Data Structure)란 데이터(정보)를 효율적으로 저장하고 관리하며, 필요한 연산을 효과적으로 수행할 수 있도록 조직하는 방법을 의미한다.

2. 자료구조 (Data Structure) 필요성

• 효율적인 데이터 저장
  • 데이터를 체계적으로 저장하여 빠르게 접근하고 사용할 수 있도록 함.
• 연산의 최적화
  • 검색, 삽입, 삭제 등의 연산을 최소한의 연산량으로 수행할 수 있도록 설계됨.
• 메모리 관리
  • 제한된 메모리를 효율적으로 사용하고 낭비를 줄임.
• 알고리즘 성능 향상
  • 알고리즘의 성능을 최적화하여 실행 속도를 높일 수 있음.

3. 자료구조 (Data Structure) 분류

3 - 1. 선형 자료구조 (Linear Data Structures)

• 데이터가 순차적으로 저장되는 구조.

(1) 배열(Array)

• 동일한 자료형의 요소들이 연속적인 메모리 공간에 저장됨.
• 빠른 접근(O(1)) 가능하지만, 크기가 고정적이고 삽입·삭제 연산이 비효율적임.

(2) 연결 리스트(Linked List)

• 데이터 노드들이 포인터를 이용해 연결됨.
• 크기가 동적으로 변하며 삽입·삭제가 용이하지만, 임의 접근(O(n))이 어려움.

(3) 스택(Stack)

• LIFO(Last In, First Out) 구조로 동작.
• 호출 스택, 수식 계산 등에 활용됨.

(4) 큐(Queue)

• FIFO(First In, First Out) 구조.
• 작업 스케줄링, 데이터 버퍼 등에 사용됨.
• 변형된 큐: 덱(Deque), 우선순위 큐(Priority Queue) 등.

3 - 2. 비선형 자료구조 (Non-Linear Data Structures)

• 데이터가 계층적 또는 네트워크 형식으로 연결됨.

(1) 트리(Tree)

• 계층적인 구조를 가지며, 부모-자식 관계로 데이터가 연결됨.
• 예) 이진 트리(Binary Tree), 이진 탐색 트리(BST), 힙(Heap), AVL 트리 등.

(2) 그래프(Graph)

• 정점(Vertex)과 간선(Edge)으로 이루어진 구조.
• 네트워크, 경로 탐색 알고리즘 등에 활용됨.
• 예) 인접 리스트(Adjacency List), 인접 행렬(Adjacency Matrix).

4. 자료구조 (Data Structure) 활용 예시

자료구조	활용 예
배열	이미지 저장, 행렬 연산
연결 리스트	메모리 할당, 데이터베이스 인덱싱
스택	함수 호출, 후위 표기법 계산
큐	프린터 작업 대기열, 프로세스 스케줄링
트리	파일 시스템, 데이터베이스 인덱스(B+ 트리)
그래프	네트워크 라우팅, 길 찾기 알고리즘 (Dijkstra, A*)

5. 임베디드 시스템 (Embedded System) 관점에서의 자료구조

메모리 최적화

• 제한된 RAM을 고려하여 링 버퍼(Ring Buffer), 연결 리스트(Linked List) 등의 동적 할당이 가능한 구조 사용.

실시간 성능 최적화

• 일정 시간 내에 동작해야 하므로 O(1) 또는 O(log n) 알고리즘을 우선 고려.
• 예: 이벤트 큐(Queue)를 사용한 RTOS 태스크 관리.

빠른 데이터 처리

• 센서 데이터 수집 및 가공을 위해 해시 테이블(Hash Table)과 우선순위 큐(Priority Queue) 사용.
• 예: Modbus 프로토콜을 처리하는 링 버퍼(Ring Buffer).

최적화(Optimization)란 알고리즘을 더 빠르게 실행하고, 더 적은 메모리를 사용하도록 개선하는 과정

• 시간 복잡도(Time Complexity) → 알고리즘이 실행되는 속도
• 공간 복잡도(Space Complexity) → 알고리즘이 사용하는 메모리 크기

자료구조는 소프트웨어 개발 및 임베디드 시스템에서 핵심적인 개념으로, 데이터 저장 및 처리의 효율성을 결정짓는 중요한 요소. 특히, 빠르고 최적화된 시스템을 설계하기 위해서는 적절한 자료구조를 선택하는 것이 필수적이다.
현재 임베디드 시스템 및 RTOS 프로젝트를 진행 중이라면, 큐(Queue), 링 버퍼(Ring Buffer), 해시 테이블(Hash Table) 등의 자료구조가 유용할 것이다. 특정 용도에 맞는 최적의 자료구조를 선택하는 것이 성능 최적화의 핵심이 될 수 있다.

6. 자료구조와 알고리즘의 연관성

자료구조(Data Structure)와 알고리즘(Algorithm)은 컴퓨터 과학의 핵심 개념이며, 서로 긴밀하게 연결되어 있음.

간단히 말해, 자료구조는 데이터를 저장하는 방식이고, 알고리즘은 데이터를 처리하는 방법.

• 자료구조: 데이터를 저장하고 관리하는 방식 (예: 배열, 연결 리스트, 트리, 해시 테이블)
• 알고리즘: 특정 문제를 해결하는 절차나 방법 (예: 정렬, 탐색, 최단 경로 탐색)

즉, "좋은 자료구조 없이는 좋은 알고리즘을 만들기 어렵고, 좋은 알고리즘은 적절한 자료구조 위에서 효율적으로 동작한다."

 

적절한 자료구조를 선택하면 알고리즘의 성능을 극적으로 향상시킬 수 있음.

7. 지수함수와 로그함수의 기본 성질

7 - 1. 지수식 (Exponential Expression)

​

7 - 2. 로그식 (Logarithmic Expression)

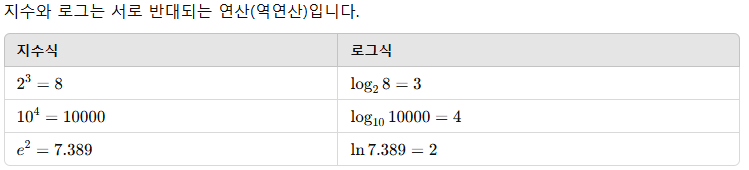
자료구조와 알고리즘에서 지수 함수와 로그 함수의 특성을 이해하면 시간 복잡도를 직관적으로 파악할 수 있음

• 지수적 증가  → 완전 탐색, 조합 문제 (비효율적)
• 로그적 증가  → 이진 탐색, 트리 탐색 (효율적)

8. 시간 복잡도 (Time Complexity)

입력 크기 n에 따라 알고리즘이 얼마나 빠르게 실행되는지 측정

• 빅오 표기법(Big-O Notation)을 사용하여 최악의 경우(Worst Case) 성능을 나타낸다.

O(1) (상수 시간)	배열에서 인덱스로 접근	입력 크기 nnn과 무관하게 일정한 시간
O(\log n) (로그 시간)	이진 탐색(Binary Search)	데이터가 증가해도 비교 횟수는 로그 비율로 증가
O(n) (선형 시간)	선형 탐색(Linear Search)	데이터가 증가할수록 실행 시간이 비례
O(n \log n) (로그 선형 시간)	퀵 정렬(Quick Sort), 병합 정렬(Merge Sort)	최적의 정렬 알고리즘
O(n^2) (제곱 시간)	버블 정렬(Bubble Sort), 선택 정렬(Selection Sort)	데이터가 많아질수록 실행 시간이 급격히 증가
O(2^n) (지수 시간)	피보나치 재귀(Brute Force)	입력 크기 nnn이 증가하면 실행 시간이 폭발적으로 증가

 

9. 공간 복잡도(Space Complexity)

알고리즘이 실행되는 동안 사용하는 메모리의 크기를 측정

• 기본적으로 입력 데이터 저장 공간 + 추가 변수 공간을 고려

공간 복잡도	알고리즘 예시	설명
O(1) (상수 공간)	변수 하나 사용	추가 메모리를 거의 사용하지 않음
O(n) (선형 공간)	배열, 리스트	입력 데이터 크기에 비례한 메모리 사용
O(n^2) (제곱 공간)	그래프 인접 행렬	데이터가 많아질수록 공간 사용이 급격히 증가